Professor Claudia Ratti from the University of Houston discusses the connection between heavy-ion collisions and astrophysical observations of neutron stars and their mergers, and the progress in the theoretical work needed to describe them.
The early Universe, just a few microseconds after the Big Bang, was permeated by a phase of matter called quark gluon plasma (QGP). In ordinary matter, quarks and gluons are ‘confined’ inside composite objects called hadrons, such as protons and neutrons. In the QGP, quarks and gluons are free to move over the whole size of the system and they do not belong to a bound hadronic state any longer. For this reason, we say that the QGP is the ‘deconfined’ phase of strongly interacting matter. The conditions under which the QGP exists are extreme – the temperature needed to melt hadrons and liberate their inner constituents is about 100,000 times the temperature inside the core of the Sun, while the density would correspond to squeezing the whole Earth into the size of a basketball. As the Universe continued expanding and cooling down after the initial explosion, a phase transition took place in which quarks and gluons were bound together into massive hadrons, which make up most of our visible Universe today.
While the confinement mechanism is not yet well understood, and in fact it is one of the Millennium Prize Problems, we know that it is due to the peculiar nature of the strong force, which has a running coupling that increases with the distance. At small distance, in the ‘asymptotic freedom’ regime, quarks and gluons are weakly coupled. The energy density needed to achieve deconfinement can be generated in the most powerful machines built by mankind – heavy-ion colliders.
The discovery of the quark-gluon plasma was announced by all four experiments at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory in 2005.1 RHIC accelerates gold nuclei at ultrarelativistic speed, makes them collide with each other and looks at the aftermath of these collisions. On an even larger scale, the Large Hadron Collider (LHC), which is situated around 100m under the city of Geneva and has a diameter of about 26km, collides lead nuclei at the highest possible energies on Earth, thus creating a long-lived QGP which is the most similar to the early Universe phase. While the QGP does not live long enough to be directly observed in the detector, which instead will observe again bound states of quarks and gluons, these hadrons will have peculiar behaviour, due to the fact that they went through a phase transition.
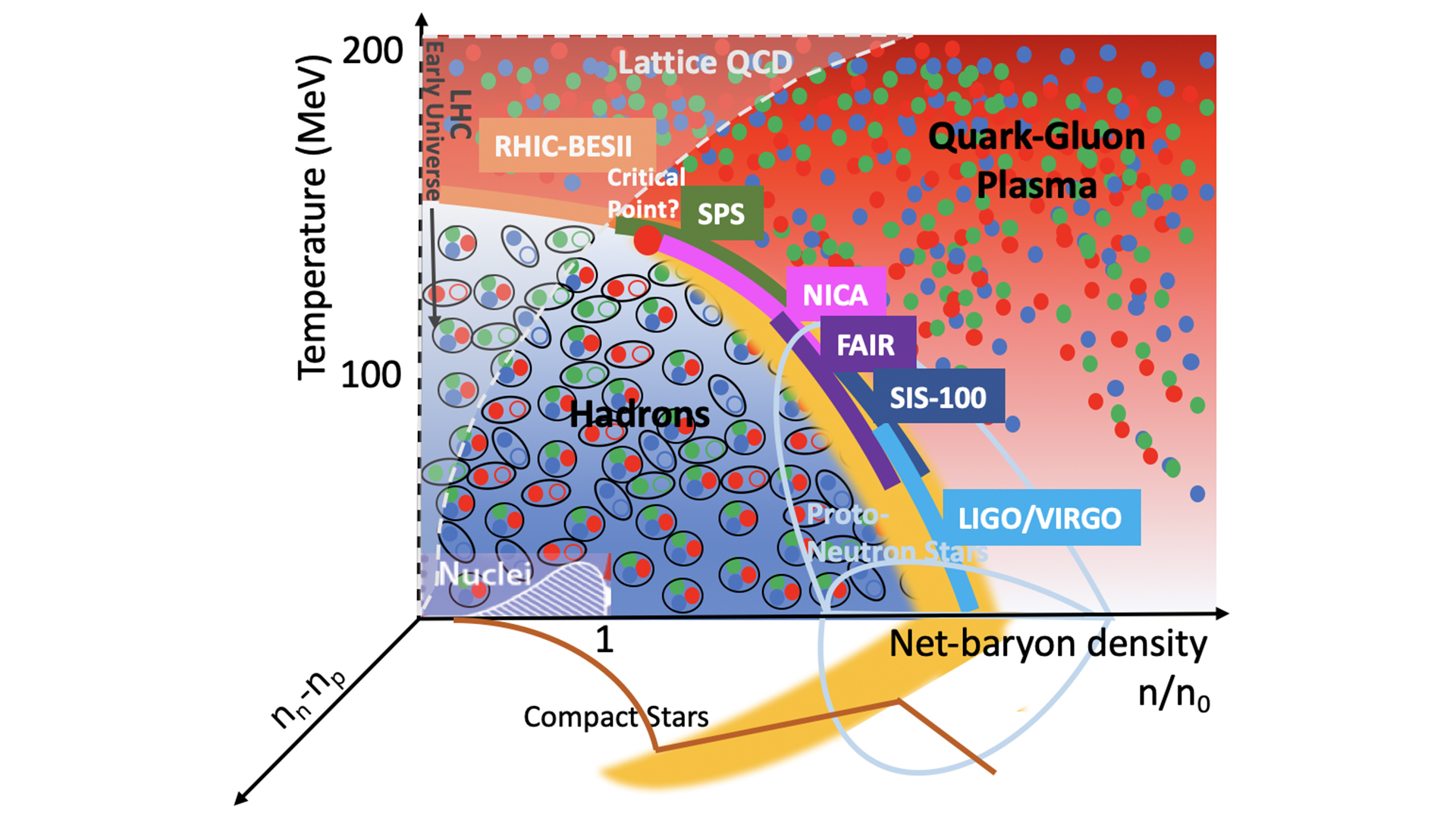
Fig. 2 shows a cartoon of the phase diagram of strongly interacting matter in the temperature and net-baryon density plane. The latter indicates the net density of matter minus anti-matter. The plane is separated by a phase boundary line, below which we have hadronic matter, and above which we have the QGP. The colourful bands indicate current and future terrestrial facilities, with the regions of the phase diagram that they are able to cover.
It is important to note that the most energetic collisions generate the most matter-antimatter-symmetric QGP. This is due to the fact that, when accelerated to relativistic speed, the colliding nuclei become Lorentz-contracted along the collision direction, meaning that, when they meet, they are effectively transparent to each other. The energy released in the collision is then turned into matter-antimatter in equal amounts. At lower collision energies, Lorentz contraction is not so strong, and nuclei have a non-negligible thickness along the collision axis. Therefore, when they meet, some of their protons and neutrons remain in the collision region, thus enhancing the matter content of the QGP and making it more baryon rich.
The exploration of the QCD phase diagram has recently gained a new player – astrophysical observation of neutron stars and their mergers. They will help to hold down the lower-right corner of the phase diagram, corresponding to large density and low temperature, which cannot be reached in terrestrial experiments. Indeed, in 2017 the LIGO/VIRGO collaboration announced its sixth gravitational wave observation. While the first five were due to the merger of two black holes, and as such were not followed by a visible signal, the aftermath of this event was seen by 70 observatories across the electromagnetic spectrum. The gravitational wave signal, named GW170817, lasted for about 100 seconds and it had the typical frequency and intensity features expected of the merger of two neutron stars. This marked a new era for multi-messenger astronomy. Nuclear physics – in particular, information on the internal composition of these stars and therefore on the cold and dense corner of the phase diagram – is encoded in every stage of the merger event. Neutron stars are very dense celestial objects: they have a mass that can be as high as twice the mass of the Sun, but a radius of just 10-15km. While a single neutron star can be considered a cold object on the scale of temperatures on the phase diagram in Fig. 2, the energy developed in the mergers can lead to temperatures, which overlap with those achieved in the lowest-energy heavy-ion collision experiments.
Matter in heavy-ion collisions: The most ideal fluid
The matter created in heavy-ion collisions presents unexpected features: it is the most ideal fluid ever observed, namely the one with the smallest shear viscosity over entropy ratio. This discovery followed from the observation of remarkable collective behaviour in the experimental data, which was subsequently described in terms of relativistic viscous hydrodynamics, with an almost negligible viscosity. These simulations need an equation of state as input – namely, they need to be informed on the thermodynamic properties of the matter of which they describe the dynamical evolution. The same is true for the simulations that describe the dynamical merger of two neutron stars. This equation of state, which is therefore a central quantity for both heavy-ion and neutron star communities, is not known from first principles over the whole phase diagram, for reasons that will be explained below.
The theory of the strong force
The theory that describes the strong force is called quantum chromodynamics (QCD) and its authors were awarded the Nobel Prize in 2004. The peculiar behaviour of QCD is due to the fact that the carriers of the force, gluons, can self-interact. This is what we call a non-Abelian gauge theory. This is different from what happens in quantum electrodynamics (QED), the theory of electromagnetism, in which photons carry the interaction between electrically charged particles but do not interact with each other. The self-coupling of gluons is the basis of the confinement mechanism and of the running of the coupling with distance.
In the regime which is relevant to study the phase transition of QCD, the coupling is too large to allow an analytical solution of the theory. The only way to solve the theory in this case is through numerical techniques, called lattice QCD. The continuous space-time in which we live is replaced by a four-dimensional (4D) discrete grid of points. Quarks are placed on the sites of this grid, gluons on the links between the different sites, and their interaction is solved numerically. Replacing the continuum world by a grid of points reduces the dimensionality of the problem: a solution of the theory in the continuum would require the calculation of an infinite number of integrals. Instead, on the lattice we have to sum a finite number of terms. However, the amount of terms would still be prohibitively large (of the order of 10^300000) even on a very small, very coarse lattice. Luckily, most of these terms can be thrown away since their statistical weight is negligible. This is done by means of Monte Carlo simulations.

Recent developments in hot and dense QCD
Whilst there has been quite some progress on mapping out the phase diagram theoretically, a large part of this map is still under construction. The same is true for the equation of state. This is due to the infamous fermion sign problem, which turns the statistical weight complex at finite density, thus making Monte Carlo simulations unfeasible. While a method to solve the sign problem has not been found yet, alternative expansion schemes have been successful in pushing our knowledge of phase diagram and thermodynamics to increasingly large density.2 Lattice QCD simulations unambiguously proved that the QCD phase transition is a crossover at small density,3 which means that it smoothly takes place over a finite range of temperatures around T~158 MeV. The shape of the transition line, as it leaves the temperature axis and extends to finite density, is also known from first principles.4
Several phenomenological models, which capture some aspects of the fundamental theory but are easier to simulate at large density, predict that the transition becomes steeper at increasingly large density, finally turning first-order, with development of a latent heat and therefore of a discontinuity in some thermodynamic quantities such as the entropy. This would mean that there is a critical point on the QCD phase diagram, separating the two phase transitions of different orders. The search for the critical point is ongoing: RHIC just concluded the data-taking for its second Beam Energy Scan, and results are expected soon.
In this search, the theoretical support is crucial. On the one hand, an equation of state in which the critical point can be inserted or removed, and its strength increased or reduced, will help to test its effect on data through hydrodynamic simulations.5 On the other hand, it is important to identify observables which are sensitive to the critical point, so that its effect can be seen in the data. The most promising ones are fluctuations of conserved charges. They are predicted to diverge at the critical point, so that a sharp peak in the data as a function of collision energy would be a clear critical point signature.6 The community is eagerly awaiting the new RHIC data on fluctuations, to determine whether these predictions are reflected in the data. Indeed, the increased statistics achieved in these new runs should allow physicists to turn promising trends into definitive conclusions on the existence and location of the elusive critical point.
Towards the high-density regime
The equation of state for neutron stars and mergers needs a range of temperatures and densities which are currently outside the reach of first principle simulations. For this reason, effective theories and models are used in this case. It is crucial that these approaches have a well-defined range of applicability, which reflects the underlying degrees of freedom, and that the model parameters are fixed to reproduce known experimental or theoretical constraints. Several different equations of state are available in this case. The next generation of gravitational wave observatories should be able to distinguish between these models, based on their imprint on the gravitational wave signal and other observables, thus leading to a way of constraining the degrees of freedom that populate the cold and dense corner of the QCD phase diagram.
Acknowledgement
This material is based upon work supported by the National Science Foundation.
References
1: K Adcox et al (PHENIX), Nucl. Phys. A 757, 184 (2005); I Arsene et al. (BRAHMS), Nucl. Phys. A 757, 1 (2005); B B Back et al. (PHOBOS), Nucl. Phys A 757, 28 (2005); J Adams et al. (STAR), Nucl. Phys. A 757, 102 (2005)
2: C Ratti and R Bellwied, Lect. Notes Phys. 981, 1-216 (2021); C Ratti, Rept. Prog. Phys. 81, 084301 (2018)
3: Y Aoki et al., Nature 443, 675 (2006)
4: S Borsanyi et al., Phys. Rev. Lett. 125, 052001 (2020)
5: P Parotto et al., Phys. Rev. C101, 034901 (2020); X An et al., Nucl. Phys. A1017, 122343 (2022)
6: M Stephanov, Phys. Rev. Lett. 102, 032301 (2009)
7: J. Biddle et al., PoS LATTICE2018 (2019) 325







