Professor Laurent Jolissaint explains how Artificial Intelligence (AI) and adaptive optics (AO) could help us see through the blur of atmospheric turbulence to gain an unlimited view of the stars.
Sir Isaac Newton famously stated that, to see the stars clearly, it is best to leave the cities and reach the mountain summits, where the air is clear of dust and trouble. In his time, light pollution was not yet a problem and there were no satellite constellations in the sky, but still, the poetic twinkling of the stars was already seen as a limitation by Sir Isaac. Far from the cities and up in the mountains meant reaching a colder air, less affected by the ground heating during the day. The great scientist realised that, what would be termed optical turbulence a few centuries later, was a serious issue.
So, what is happening in the air tonight? Air temperature decreases with altitude and, when blown by the wind, cold or warm air masses are mixed into a turbulent flow. Now, the refractive index of air depends on its temperature. Therefore, the turbulent air flow generates what is called a turbulent field of refractive index. To explain, if you look at a star through atmospheric turbulence, the light ray will constantly jump here and there and will miss your eyes. You will get this impression of twinkling. If you take a long exposure picture, though, the twinkling will be averaged, but the image will be blurred anyway. Fig. 1 illustrates the effect.
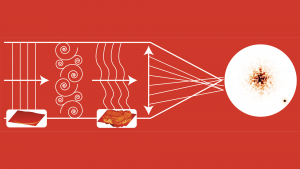
On a good site, the star image will be a speck of light with an angular extension of about one arc-of-a-second, i.e. 1/3600 of a degree. This is tiny – the Moon angular diameter is 0.5 degree, but very well noticeable even on an amateur telescope. Fig. 2 gives a sense of what the image degradation is due to a 1 arc-second optical turbulence. This is enough to blur the image of the things that are really interesting in the sky, such as details on the planets of our Solar System for example. In fact, this angular resolution is the same as what a domestic telescope of 10cm will give you if there was no turbulence.
With turbulence, large ground-based telescopes (the Keck telescope is 10m in diameter) are myopic. However, it is still worth constructing large telescopes, because the larger their diameter, the more light they catch and the further away we can see in the Universe.
Sending the telescopes to space is the easiest answer. However, the cost and physical challenges attached to a space telescope do pose limitations. Sending a telescope of around 40m in diameter – the diameter of the European Extremely Large Telescope (ELT) – into orbit is not currently in reach. So, for now, we are restricted to the ground.

Babcock: An astronomer ahead of his time
In 1953, American astronomer Horace W Babcock devised a theoretical solution.1 If the optical wavefront aberration generated by turbulence could be measured, then this could be used to wrap a reflective device into a shape such that, after reflection, the aberrated beam would be corrected. The optical system would adapt itself to the turbulence. The idea of adaptive optics was born.
Unfortunately, there was no device available at the time for implementing this concept in an efficient manner. Babcock did identify a wavefront sensing (WFS) solution and a sort of corrector, but the idea was never implemented, possibly because of the low expected performance and the applicability restricted to a few bright stars. Nevertheless, the idea was noted and came to fruition 30 years later, under the independent efforts of both astronomers and the military, thanks to the availability of fast digital detectors, computers, and the development of active, deformable mirrors.2
The pioneers
Surprisingly for the astronomical community, the US military later declassified their own adaptive optics (AO) research, as the civil systems were reaching the same level of performance. COME-ON produced the first diffraction limited image from a star on a large telescope.3 The AO concept was then validated, on sky. Fig. 3 shows the level of performance reached by classical AO systems, in this example on an 8m telescope (VLT, ESO).

Since then, the improvement has been massive, but there has been no fundamental change in the concept. AO has become a new technology, with its own universe, and applications are slowly leaking to other fields of optics – in particular, ophthalmology and ground-space communication. Generating artificial guide stars with laser beams, to ensure that a guide star is available near the science object, and using several deformable mirrors to compensate a larger field-of-view are certainly the most significant improvements since COME-ON.
The loop delay in AO systems
Measuring and computing the wavefront aberration takes time and, during this time, the wind continues to blow, so when the correction is applied, there is some difference between the current aberration and the applied correction. The delay is equal to the exposure time of the WFS, plus the detector reading, and the correction computation time. We may imagine, using the powerful computers of the future, that the calculation delay could become virtually zero, but not the exposure time, because we need to let enough photons into the detector to get some measurement: no light means no data. Again, ideal sensors can be imagined – no reading time, no technical noise – but exposure time cannot be zero. This delay error is an issue in the case of the highest degree of AO correction, for exoplanet research: the residuals from the atmosphere create speckles of light that resemble a planet signal, making the data processing challenging.
This is where predictive control comes in. If a turbulent flow is in a given state, its evolution cannot be fully random, because air masses have some inertia. Therefore, from a given aberration, it must be possible to predict its evolution between the end of the exposure and the application of the correction, and compensate for the delay error. This has been tested by several groups already4 and shows some promise. The difficulty is that an accurate model of the AO system elements is required, as well as a good statistical model of the turbulence itself.
Finite spatial sampling
The other serious limit of an AO system is the finite spatial sampling of the wavefront error, i.e. the number of data points you measure in the optical beam.The thinner the measurement grid on the pupil (an image of the primary mirror), the better the correction. However, if the spatial sampling is pushed too high, the number of available photons on each sampling element becomes too low, and the correction quality degrades. Increasing the length of exposure time may look like the solution, but then we lose track of the turbulence, again causing a delay. So, for a given guide star brightness and turbulence strength, there is an optimal spatial sampling for the WFS. If the observing condition changes, however, the optimisation is no longer valid.
A solution lies in a new type of WFS: the pyramid WFS (P-WFS). At the core of the sensor is a pyramidal prism, splitting the light beam into four – each providing an image of the telescope pupil. By combining these images in a certain way, – we may not enter into the details here – it is possible to obtain a measurement of the wavefront error, basically a map of the hills and valleys of the wavefront error – as shown in the insert in Fig. 1. 5 The excellent features of this sensor are that its measurement range can be adjusted to the amplitude of the wavefront and that its spatial resolution can be adjusted. If aberration is strong but the light level is high, for example, a wide measurement range and fine resolution can be selected. If the aberration is weak and there are not many photons, the measurement range can be lowered and the spatial resolution increased. This can be done while the correction is ongoing. This is completely new in AO and opens many possibilities.
TROIA: A flexible and autonomous adaptive optics system driven by AI
TROIA is the new TuRkish adaptive Optics system for Infrared Astronomy. It is built to equip DAG, Turkey’s new four-metre telescope, and will compensate optical turbulence at a very fine scale, allowing research in the field of extra solar planets. It has been developed by our optical instrumentation team at the School of Business and Engineering of Canton de Vaud (HEIG-VD), a member of the University of Applied Science Western Switzerland (HES-SO).
We decided to use the best state-of-the-art technology for TROIA core components. A high-resolution P-WFS was selected, paired with a high actuator density deformable mirror (DM). Thanks to the versatility of the sensor, it is possible to systematically choose the optimal measurement range and resolution for a given turbulence condition. With these technologies, the ultimate correction quality can be achieved.
Unfortunately, we still have the loop delay problem and a way to select the optimised system parameters – range and resolution – has yet to be found. However, we think this issue could be aided by Artificial Intelligence (AI) at two levels. The first level relates to the choice of the system parameters: the loop speed (the temporal frequency at which the correction is done) and the amount of correction you want to apply, considering the measurement noise – the loop gain. It is rather intuitive that the faster the wind, the faster the loop has to run, and it is also easy to understand that, if the star brightness is low, a longer exposure time is needed, which makes the loop frequency lower. This optimisation process – a version of which is called modal control – is well known and implemented in adaptive optics systems.
With the P-WFS flexibility, the high number of actuators and the noiseless camera of TROIA, the space of parameters to adjust becomes larger. It makes four parameters to optimise: loop frequency, loop gain, measurement range and resolution. Loop gain may actually become a more complicated object, depending on the spatial scale of the aberrations. We may want to compensate with more trust the aberrations for which we have a good measurement quality, and less, or not at all, the aberrations at high spatial scales for which the measurement quality is lower.
There may be mathematical models to compute, at each instant, what the optimal values of the four parameters are, but the models will only make a difference if they represent well the physical reality of the whole system. This requires a high accuracy characterisation of the optical system, and the system must not change after characterisation. These conditions are difficult to meet with certainty, as some subtle effects might be unseen, or difficult to model. Modelling errors are a known problem when trying to simulate the point source image given by an AO system, and compare it with the PSF measured on sky. When the conditions are less favourable, discrepancies appear.
The concept of using AI to help is relatively simple. We would subject TROIA to a large diversity of turbulence and star brightness conditions and explore the correction performance as a function of the four system parameters, selected from a relatively simple model. The three elements: turbulence and star parameters, AO parameters, and performance are kept to generate a learning set. At the beginning, it is not optimal, in a sense that the four parameters have not been adjusted carefully. Then, at each run, the system shall use its learning set to select the four parameters, but with some random variation. If the performance is better, the previous optimal choice in the learning set is replaced, leaving a large optimised database, on which a neural network (NN) can be trained.
It would seem that, if the database could be built, then it can simply be used, and a NN is not needed. This is almost true but the problem is that the database will never be complete, then for a given turbulence/star condition we might need some model – naturally limited – to interpolate between data. A NN can do this better and faster. If we have a large and diverse enough training set, a NN can propose a good solution, even if it does not initially exist in the database. Finally, nothing can prevent looping this process with the continuous addition of the best parameter selection in the learning base. The older the system, the wiser.
This idea is illustrated in Fig. 4, where the NN constantly learns by analysing the performance as a function of the system parameters and the optical turbulence.
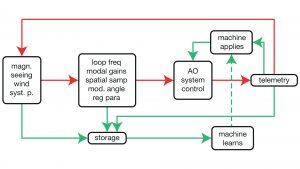
At the end, the system would simply look at the WFS data, and be able to identify how to adjust the loop parameters automatically, continuously. This is an automatically adaptable adaptive optics system.
The second level of AI takes care of the loop delay problem. As previously stated, because turbulence evolution is set by the fundamental laws of physics, conservation of energy and inertia, it cannot jump randomly from one state to another. Therefore, if the optical aberration has a certain structure at a given time, by applying the laws of physics, we would be able to, in theory, predict what is next and use it at the moment of the correction.
This is only partly possible, for many reasons. Firstly, the measurement is never perfect and, because the turbulence has a chaotic nature, a small error on the measurement can lead to a large prediction error in the immediate future. Secondly, due to the turbulent nature of the flow, it is virtually impossible to build a physical model that would predict the aberration evolution. What is left is the aberration evolution statistics. Temporal correlation models of optical turbulence aberration exist and can be used to predict the most probable evolution of a given aberration at a given time. But, as we can guess now, the quality of the prediction will depend on the quality of the model, and the measurement.
NN could potentially solve this problem. With TROIA, we could keep all the aberration measurement history, at each instant. From this large database, we can determine, for each aberration configuration at a given time, the next evolution at an instant later. Obviously, this would have to be done for stable turbulence/star conditions. Then, a NN can be trained with these two sets – aberration at t1 as an input and aberration at t2 as the output. The NN would then be able to predict, for a given aberration, the most probable aberration an instant later, and use this value to compensate the aberration.
If you imagine the two NNs working together, the loop starts with basic presets. NN-1 pauses, observes the aberration statistics, and decides to set up the AO loop parameters at the optimal value. Then, it would tell NN-2 what the current turbulence/star conditions are. NN-2 would then select the appropriate learning set and use its knowledge to predict the best correction from each measurement of the P-WFS.
We believe this is the future of adaptive optics. Indeed, these systems are complex, and constructing reliable models on which we can rely to predict turbulence and take the best decision is inevitably limited by our fundamental inability to build such models with completeness. However, because AO systems are governed by the laws of physics, the same turbulent input for a given AO setup should produce the same outcome – for example, the same correction command. Therefore, a neural network can be trained from the empirical data.
There is always truth in the data, while a model is always incomplete. Data-based control instead of model-based control is a real, fundamental change of paradigm in AO. The AI creates its own internal logic – which we do not have access to – to link a given input to an expected output. TROIA, left alone with the measurements, will decide itself how to compensate turbulence. The astronomer will have more time to think about pure science.
References
1 The Possibility of Compensating Astronomical Seeing, Horace W Babcock, PASP, 65, 386, p. 229, October 1953
2 Adaptive optics components in Laserdot, Pascal Jagourel, Jean-Paul Gaffard, Proc. SPIE 1543, January 1992
3 First diffraction-limited astronomical images with adaptive optics, G Rousset et al., A&A, 230, 2, L29-L32, April 1990
4 Predictive wavefront control for adaptive optics with arbitrary control loop delays, Lisa Poyneer and Jean-Pierre Véran, JOSA A, 25, 7, June 2008
5 R. Ragazzoni, “Pupil plane wavefront sensing with an oscillating prism,” J. Modern Opt. 43, pp. 289—293, 1996
Please note, this article will also appear in the tenth edition of our quarterly publication









