The theory of fermion condensation offers an unexpectedly simple and reliable description of strongly correlated Fermi systems.
The Landau Fermi-liquid (LFL) theory has a long history and brilliant accomplishments in describing the diverse properties of an electron liquid, ordinary metals and Fermi liquids like 3He. This theory is built on the assumption that the physics at low temperatures defines elementary excitations that behave like quasiparticles, characterised by their effective mass M* and belonging to the same class of weakly interacting Fermi gas. The effective mass M* depends weakly on temperature (T), pressure (P), and magnetic field (B).
Strongly correlated Fermi systems, a new state of matter, have received attention from modern fundamental physics. These systems are represented by high-temperature superconductors, heavy-fermion (HF) metals and quantum spin liquids (QSL) as well as systems such as two-dimensional (2D) 3He and quasicrystals. The behaviour of strongly correlated Fermi systems, not describable within the LFL standard picture, still requires theoretical explanation.
This relatively novel class of strongly correlated Fermi systems exhibits a huge variety of physical properties. The properties of these materials are fundamentally different from those described by ordinary LFL. Characterised by strong electron correlations, strongly correlated Fermi systems require the renormalisation of the effective mass M* of quasiparticles, which can exceed the bare mass by several orders of magnitude or even become infinitely large. In this case, the effective mass is highly dependent on temperature, pressure or applied magnetic field. Thus, these systems exhibit the non-Fermi liquid (NFL) behaviour that can be explained within the framework of the strongly correlated systems theory, which is based on the topological fermion condensation quantum phase transition (FCQPT), leading to a quite specific state called fermion condensation (FC).1-5
As an indicator of FCQPT, unlimited increase of M* determines the excitation spectrum and creates flat bands. The theory of FC describes completely the non-Fermi liquid (NFL) behaviour of strongly correlated Fermi systems. Moreover, FC can be considered as the universal reason for the NFL behaviour observed in various HF metals, 2D 3He liquid, compounds with quantum spin liquids, and quasicrystals.3-6 We show that these systems exhibit universal scaling behaviour of their properties, as it is demonstrated within the framework of the International Laboratory ‘Fermion Condensation’ (http://fc.komisc.ru/inde
x.php?incl=home). Therefore, the quantum critical physics of different strongly correlated compounds is universal, and emerges regardless of the underlying microscopic details of the compounds. This uniform behaviour, governed by the universal quantum critical physics and induced by the same FCQPT, allows us to view these strongly correlated Fermi systems as a new state of matter.
Weakness and strength of correlations
The concept of correlation is introduced in mathematical statistics through formulas; however these are unnecessary for our presentation. We restrict ourselves to an example, hoping that visualisation of this concept allows us to understand it at an intuitive level. Fig. 1 shows a huge flock of starlings, moving in such a coordinated (correlated) manner that, in addition to the forces of attraction to the ground and the forces of interaction with air, a certain collective force acts on the birds, giving the flock a complex shape and controlling its transformation.
We know that the reason for this phenomenon lies in the psychology of behaviour (not only birds, but also fish and insects can behave in this manner). During their flight, the starlings not only struggle with gravity and air resistance, but also control the distance to their nearest neighbours (maintain a constant density of the flock), and also repeat their manoeuvres. Considering errors and external disturbances, the pack behaves as a single system controlled by a correlation interaction distributed over its volume.
The substance surrounding us consists mainly of electrons, protons and neutrons that are fermions. Combining in related groups, fermions can form bosons or fermions again, for example, this is how bosons (helium atoms 4He or fermions) 3He are obtained. All particles are divided into two classes: bosons having an integer spin (1, 2, etc.), and fermions carrying a half-integer spin (1/2, 3/2, etc.). This difference determines their collective behaviour, in particular if there can be any number of bosons in one state. Then according to the Pauli principle, the number of fermions in one state cannot exceed two, and they must have oppositely directed spins.
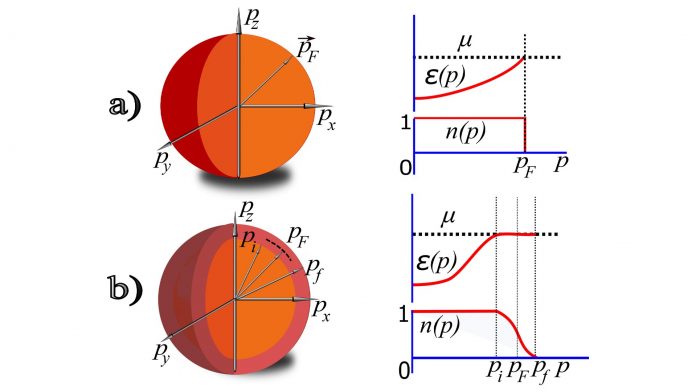
For example, at absolute zero temperature, free bosons will gather at the lowest energy level, forming a system called bosonic condensate, while under the same conditions, fermions will successively fill a certain set of lower states, forming a structure that has the form in the momentum space spheres, see Fig. 2 (a). L.D. Landau changed Dirac’s observation in his own way, noting that the properties of Fermi liquids are determined by their excitations, the most important of which are quasiparticles. Quasiparticles, like particles, have a mass M*, which is called effective, charge and spin. The content of the LFL theory is that it is the quasiparticles that determine the thermodynamic, transport, and other properties of Fermi fluids. In the LFL theory, it is fundamental that the quasiparticles influence each other so weakly that they behave more like an ideal gas than a liquid.
Therefore, it was relatively easy to consider their interaction with each other and with external fields. Consequently, M* turned out to be of the same order as the mass of the fermions that form the liquid and does not strongly depend on temperature, the applied magnetic field, or other external factors. Over the past 30 years, a new class of materials has been discovered and studied; ‘the strongly correlated Fermi systems’. Their behaviour is fundamentally different from normal Fermi fluids and cannot be described within the framework of the Landau theory. The effective mass of quasiparticles turns out to be hundreds and even thousands of times larger than the ‘bare’ mass of an electron – it substantially depends on temperature, magnetic field, and other external fields. As a result, one could surmise that quasiparticles become heavy and die or simply vanish.7 Since quasiparticles determine the main properties of Fermi systems, the entire behaviour of strongly correlated Fermi systems, including high-temperature superconductors, metals with heavy fermions, 2D 3He, quasicrystals, and quantum spin liquids, becomes inexplicable provided that the quasiparticles vanish.
Metamorphoses at low T
To understand the essence of the phenomena occurring in these substances, let us consider several ideas related to the symmetry of many body systems. By symmetry is understood the invariance of the properties of a physical system, manifested during any changes or transformations. For example, the spherical symmetry of a body means that the appearance of the body does not change if it is rotated in space at arbitrary angles. The same thing happens with ordinary matter: at a sufficiently high temperature, it is in a state with a maximum degree of symmetry (e.g. gaseous). During cooling, as a result of thermal processes, a change in symmetry occurs – an ordering, which can manifest itself in the appearance of a crystalline structure. When absolute zero is reached, the resource of generation of new states due to thermal processes is exhausted.
However, even at T = 0, phase transitions are possible. These phase transitions are called quantum phase transitions. Among which are the topological phase transitions transforming the Fermi surface and considered in the pioneering works of Ilya Mikhailovich Lifshits. Consider a topological phase transition that separates a normal Fermi liquid from a strongly correlated Fermi liquid. If the system of free Bosons at T = 0 is represented in the momentum space as a point at the origin, all particles occupy a state with zero energy and momentum, then the system of free Fermi particles occupies the volume bounded by the Fermi sphere. The Fermi sphere has a two-dimensional surface – a surface of constant energy; its sharp external boundary at zero temperature separates free and occupied states. A schematic representation of the momentum distribution function of quasiparticles n(p) at T = 0 is shown in Fig. 2(a).
A sharp boundary of the Fermi sphere means the absence of quasiparticles outside the sphere and corresponds to a stepwise termination of the function n(p) for some momentum p = pF, called the Fermi momentum. The energy of quasiparticles ε(p) monotonically increases with increasing momentum and is equal to µ, the chemical potential at p = pF. In this picture, correlations between particles are not yet strong. Quantum correlation effects in the Fermi system can be influenced by several factors. The chemical composition of the compound can be specially selected. The phase transition can be controlled by applying a magnetic field or pressure to the system, and the radius of the Fermi sphere can be changed by simply altering the concentration of quasiparticles.
In all cases, it is necessary to ensure that the ratio of the kinetic energy, that maintains chaos in the system, to the energy of both the electrostatic interaction and of correlation interaction, that generates collective effects, decreases. When its fraction becomes sufficiently small, the relative contribution of kinetic energy decreases, which can be represented as an increase in the effective mass, for the kinetic energy is back to being proportional to M* that goes into unlimited growth and leads to a phase transition. This phase transition, minimising the correlation energy, turns the Fermi surface into a Fermi volume in which all quasiparticles acquire at T = 0 the same energy equals µ, as shown in Fig. 2(b). The quasiparticles of the Fermi volume are in different equilibriums, and a separate quasiparticle ‘travels’ in this volume without changing the energy. As a result, the system acquires the NFL behaviour.4
Such a quantum phase transition, essentially topological, is connected with the transformation of the Fermi sphere, which is transformed from a two-dimensional manifold into a three-dimensional one. The transformation of the Fermi sphere as a result of such a phase transition is shown in Fig. 2(b). This phase transition is stable against deformations of the Fermi sphere.2 It can be seen from Fig. 2(b) that the Fermi sphere decays into two subsystems: the inner part of the sphere remains unchanged, and the Fermi surface becomes three-dimensional (the quasiparticles of this three-dimensional shell have the same energy in the pulse interval from pi to pf, and their distribution function continuously changes from 1 to 0). Since the quasiparticles of the swollen shell have the same energy, the authors of this discovery introduced the name ‘fermion condensate’.1,4
With fermion condensate and Bose condensate, they both have a macroscopic number of quasiparticles combined (condensed) in one group, characterised by the same energy for all particles. For Bose condensate this is the energy of the deepest state, and for fermion condensate it is the energy of the Fermi surface. Thus, the Fermion condensate creates the same density of states in the Fermi volume as the Bose condensate at low energy. However, the Bose system behaves significantly differently; it becomes completely ordered at zero temperature. The quasiparticles of the Fermi system located in the fermion condensate can move from one state to another without changing the energy within the momentum range (pf − pi), (see Fig. 2(b)). Therefore, all of the time they ‘maintain disorder’, which leads to numerous phase transitions ‘swallowing’ FCQPT at low temperatures.4
New state of matter
At low temperatures, and under the application of magnetic field B, the effective mass M* of quasiparticles is constant – the magnetic field is strong enough to destroy the strongly correlated state and restore the LFL behaviour. Then, with increasing T, M* reaches a maximum and begins to decrease. This transition region corresponds to the weakening of the magnetic field and separates the LFL behaviour from the NFL one, namely, M* begins to depend on temperature. From the theory of FC it follows that M* has the universal scaling property.3-5 Note, the effective mass defines the main properties of the system. If we normalise the specific heat C/T ∝ M* to its value at some point, for example, at the maximum point, and the temperature, respectively, to the value at which C/T is maximal, we obtain two dimensionless quantities: the normalised effective mass MN* and the normalised temperature TN.
Then the FC theory states that the behaviour of such a function MN*(TN ) will be described by some universal function, determining the properties of the system. This function does not depend on the chemical composition of the sample, on the magnetic field, on the density of quasiparticles, etc.4,5 Fig. 3 shows normalised effective mass MN* extracted from measurements on different HF metals; as expected, MN* reveals the universal scaling. As can be seen from the figure, the scaling behaviour is preserved – all the curves coincide with each other when the normalised temperature changes by more than two orders of magnitude.
Analysis of the experimental data within the framework of the FC theory showed that a quasicrystal of this type behaves similarly to HF metals.4,5 Thus, we conclude from both the experimental and the theoretical points of view that strongly correlated Fermi systems exhibit the universal scaling behaviour of their properties, formed by the topological FCQPT; therefore, they form the new state of matter.4,5,6
In summary, the successful explanation of the diverse properties of HF metals, quantum spin liquids, quasicrystals, and a number of other substances like 2D 3He, indicates that the theory of FC offers an unexpectedly simple and reliable description of strongly correlated Fermi systems. These have been transformed from rare laboratory samples into a wide class of new, technologically promising and a wide variety of materials that form the new state of matter. They thus open a new page in modern condensed matter physics. Much of this work is carried out within the framework of International Laboratory ‘Fermion Condensation’ (see: http://fc.komisc.ru/index.php?incl=home). This Laboratory represents an example of effective and successful approach to solving complicated problems of modern physics.
References
- A. Khodel and V. R. Shaginyan. 1990. Superfluidity in system with fermion condensate, JETP Lett. 51, 553
- E. Volovik. 1991. A new class of normal Fermi liquid, JETP Lett. 53, 222
- R. Shaginyan, A. Z. Msezane, K. G. Popov, and V. A. Stephanovich. 2008. Universal Behavior of Two-Dimensional 3He at Low Temperatures, Phys. Rev. Lett. 100, 096406
- R. Shaginyan, M. Ya. Amusia, and A. Z. Msezane et al. 2010. Scaling Behavior of heavy fermion metals, Phys. Rep. 492, 31
- R. Shaginyan, V. A. Stephanovich, and A. Z. Msezane et al. 2017. New State of Matter: Heavy Fermion Systems, Quantum Spin Liquids, Quasicrystals, Cold Gases, and High-Temperature Superconductors, J. Low Temp. Phys. 189, 410
- R. Shaginyan, A. Z. Msezane, and M. Ya. Amusia, et al. 2019. Thermodynamic, Dynamic, and Transport Properties of Quantum Spin Liquid in Herbertsmithite from an Experimental and Theoretical Point of View, Condens. Matter 4, 75
- Custers et al. 2003. The break-up of heavy electrons at a quantum critical point, Nature 424, 524
- Takahashi et al. 2003. ac susceptibility and static magnetization measurements of CeRu2Si2 at small magnetic fields and ultralow temperatures, Phys. Rev. B 67, 180407(R)
- Oeschler et al. 2008 Low-temperature specific heat of YbRh2Si2, Physica B 403, 1254
- W. Rost et al. 2011. Thermodynamics of phase formation in the quantum critical metal Sr3Ru2O7, Proc. Natl. Acad. Sci. USA 108, 16549
Co-Authors
V R Shaginyan,1, 2 A Z Msezane,2 and
M Ya Amusia3
Petersburg Nuclear Physics Institute of NRC
Kurchatov Institute
Clark Atlanta University
Racah Institute of Physics, Hebrew University
V R Shaginyan
Clark Atlanta University
+1 404 880 8663
vrshag@thd.pnpi.spb.ru
Tweet @CAU
www.cau.edu/school-of-arts-and-sciences/physics/research-centers.html
Do you want the latest news and updates Innovation News Network? Click here to subscribe, and make sure to stay connected with us.