Bretislav Friedrich, Dudley Herschbach, Sabre Kais and Burkhard Schmidt show that molecules enhanced by electromagnetic fields gain new capacities.
Molecules can sense external electromagnetic fields by their electric and magnetic moments. While electric moments arise primarily from the nonuniform electron distribution within the molecules, molecular magnetic moments are mainly due to the electrons’ angular momenta.
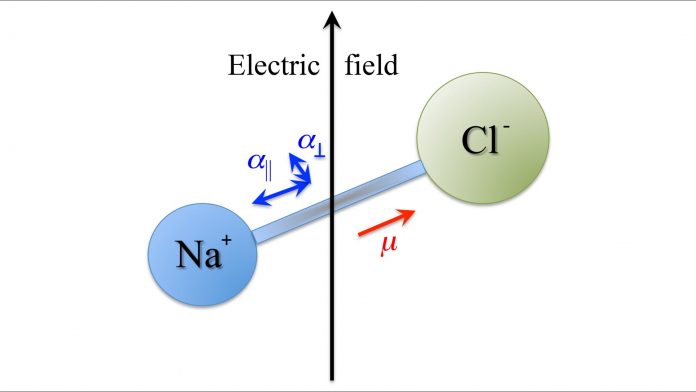
Comprised of ponderous nuclei held together by nimble electrons, molecules come in all shapes and sizes. Some of the shapes foster nonuniform electron distributions while others prohibit them. For instance, the nonuniform electron distribution in a diatomic molecule consisting of two unlike atoms, such as sodium chloride (NaCl), gives rise to an electric dipole moment: the chlorine (Cl) atom has a greater affinity (attraction) for electrons than sodium (Na) does, and as a result the electron distribution is biased, with more (negative) electron charge concentrated on chlorine than on sodium.
This makes the NaCl molecule polar, with its permanent electric dipole moment (μ) fixed along the molecular axis, which runs through the atoms’ nuclei. An external electric field can then latch on to the dipole – and thereby to the molecular axis – and orient it in its direction. When a molecule is non-polar (i.e. does not possess an electric dipole moment – benzene is an example), it can still respond to an external electric field. This is because an electric field can induce a dipole moment in a molecule – whether polar or non-polar – which can then be acted upon by the very electric field that induced it.
The induced dipole moment depends on the molecule’s polarisability, which is a measure of how tightly the molecule’s electrons are bound within the molecule. If the polarisability is uneven (anisotropic) over the molecular frame like it is for the example of benzene – which has a larger polarisability within the plane (α||) of the ring than perpendicular to it (α⟂) – the induced dipole moment is again molecule-fixed and, like the body-fixed permanent dipole moment, can be used as a lever to align the axis of the molecule.
However, in order to make the induced dipole sizeable, a strong electric field has to be applied (on the order of ten thousand kV/cm), such as that carried by an intense electromagnetic wave generated by a laser (of an intensity of the order of a billion kW/cm2). In contrast, electrostatic fields are much less strong (feasible just up to about 100 kV/cm). We note that the fields needed in order to manipulate molecular rotation are still a thousandfold weaker than the fields inside the molecules that partake in molecular bonding.
Manipulating molecular rotation
Field-free molecules rotate in space with their axes zipping through all directions. Orienting or aligning the molecular axis by an external field then amounts to manipulating the rotation of the molecular axis, turning it into a single-headed arrow in case of orientation or a double-headed arrow in case of alignment.
The ability to manipulate molecular rotation is a highly desirable feat with applications in research areas as diverse as reaction dynamics, higher harmonic generation, molecular orbital imaging, the focusing and trapping of molecules, and quantum simulation and computing. In any of these, the molecular motions (translational, electronic, vibrational, and rotational) have to be controlled to some degree in order to either investigate molecules and their interactions or to harvest their quantum properties. Herein, we outline the principles of molecular orientation and alignment as well as of shaping of rotational wavepackets as the basic means for manipulating molecular rotation. We conclude with a vignette about quantum computing with arrays of trapped molecules.
Our approach to orienting molecules, introduced in 1999, is based on combining a static electric field that acts on the permanent dipole and a non-resonant laser field that creates an induced dipole and also acts on it. The orientation occurs for any polar molecule, as only an anisotropic polarisability, along with a permanent dipole moment, is required. This is always available in polar molecules. Thus the ‘combined interactions’ technique (via the permanent and induced dipoles) is quite versatile, applicable to essentially any polar molecule. The strong orienting effect of the combined interactions arises from the tight alignment of the molecular axis by the laser field acting on the induced dipole (double-headed arrow) and its conversion to orientation by the electrostatic field acting on the permanent dipole (single-headed arrow).
The time over which the external field acts on a free-rotating molecule is of key importance: if the field is turned on and off slowly with respect to the molecule’s rotational period, the molecule continues rotating as if no interaction with the field had taken place. This is independent of how dramatic the effects of the field (say in terms of orientation/alignment) may have been during the time that the field was on.
In contrast, if the field is turned on and off ‘suddenly’ (i.e. over a time much shorter than the molecule’s rotational period), then the orientation/alignment will recur indefinitely after the turn-off of the field, at times that are related to the molecule’s rotational period (in practice, when the molecule collides, say, with the wall of the vacuum chamber, the recurrences cease as other processes take over). Hence molecules that suffered a sudden ‘kick’ exhibit orientation/alignment even in the subsequent absence of a field.
Unipolar electromagnetic pulses
Current semiconductor technologies make it possible to produce electromagnetic pulses that consist of only a single oscillation cycle of an electromagnetic wave. Moreover, the wave’s electric field distribution over the cycle can have a bias, with a higher oscillation amplitude in, say, the positive direction than in the negative one. Such ‘unipolar’ pulses turned out to be a boon to manipulating molecular rotation:
- Their short duration (typically less than a picosecond, as compared to nanosecond rotational periods of typical small molecules) ensures a sudden interaction that results in recurring orientation/alignment; and
- The pulse interacts simultaneously with both the permanent and induced electric dipole moment of the molecule, thereby automatically implementing the combined interactions technique of manipulating molecular rotation.
The figure shows a ‘population quilt’ of the rotational states (J) of a polar, and polarizable, diatomic molecule that is excited by the permanent and induced dipole ‘kicks’ of varying strength. Initially, the molecule is in its rotational ground state, J=0. The orientation and alignment of the molecule’s axis results from the superposition of the J-states excited. The effects of the permanent dipole interaction alone can be seen near the ordinate: with increasing kick strength, the quantum number of the most occupied level increases, J=0, 1, 2, …, which is in keeping with the quantum selection rule ΔJ=±1. For the case of the induced dipole interaction alone, shown near the abscissa, the sequence of the levels with the highest population becomes J=0, 2, 4, …, in accordance with the selection rule ΔJ=±2. However, quite a counterintuitive behaviour is found when the permanent and induced dipole kick strengths are the same (see the diagonal): the most populated states are those with J=0 and J=1 that alternate as the kick strength is increased. Such behaviour not only shows that the combined interactions give rise to sui generis effects (not all of them fully understood yet) but also offers itself to experimental testing.
Quantum computing
The non-resonant optical field can be also used to trap molecules via the attractive induced dipole interaction in a spatial array called an optical lattice. It was recognised by David DeMille in 2003 that an array of trapped polar molecules could be used as a platform for quantum computing. Quantum computers take advantage of the quantum phenomena of entanglement and superposition to achieve the so-called ‘quantum supremacy’ – the ability to solve problems that are either beyond the reach or the efficiency of classical computers. Such problems include factorisation and database searches, as well as dealing with many-body problems such as those arising in chemistry and condensed-matter physics and that scale exponentially with the size of the system (e.g. the number of electrons involved).
Each polar molecule trapped in one site of the optical lattice acts as a qubit entangled with other molecules of the lattice via the electric dipole-dipole interaction between the polar molecules’ permanent electric dipole moments. These qubits are encoded in the molecules’ rotational states oriented by a superimposed electric field. The actual computation is performed by applying the so-called ‘gate operations’ to the qubits by an external electromagnetic field that is resonant with transitions between the qubit states (typically a pair).
In our work from 2011 onwards, we have established proper conditions for an efficient operation of quantum logic gates using microwave pulses, and we have also identified a type of molecule (symmetric top) that allows for an exact mapping onto a nuclear spin chain, for which nuclear magnetic resonance (NMR) quantum computing techniques are well developed.
Recently, we presented methods for realising quantum computation in the gate model, the measurement-based model, and the adiabatic model, all using polar molecules. We have also shown that the control of precision of a quantum computer based on an array of trapped polar molecules would exceed that of a D-Wave 2X system by about two orders of magnitude. This could be used to perform predictive electronic structure calculations of large molecules. We note that the ability to prepare an N-molecule (with N >100) entangled state would not only benefit quantum information processing, but also quantum metrology, for instance to detect single microwave or infrared photons.
Thus, molecules enhanced by electromagnetic fields gain new capacities.
Co-authors
Prof Dr Bretislav Friedrich
Fritz Haber Institute of the Max Planck
Society (Germany)
+49 30 8413 5739
bretislav.friedrich@fhi-berlin.mpg.de
www.fhi-berlin.mpg.de/mp/friedrich/
Prof Dr Dudley Herschbach
Department of Chemistry and
Chemical Biology
Harvard University (USA)
+1 617 495 3218
hbach@chemistry.harvard.edu
https://faculty.chemistry.harvard.edu/dudley-herschbach
Prof Dr Sabre Kais
Depertments of Chemitsry, Physics, and Computer Science
Purdue University (USA)
+1 765 494 5965
kais@purdue.edu
https://www.chem.purdue.edu/kais/
Dr Burkhard Schmidt
Institute of Mathematics
Freie Universität (Germany)
+49 30 838 51382
burkhard.schmidt@fu-berlin.de
https://sites.google.com/site/quantclassmoldyn/team/current/burkhard-schmidt
Fritz Haber Institute of the Max Planck Society (Germany)
+49 30 8413 30